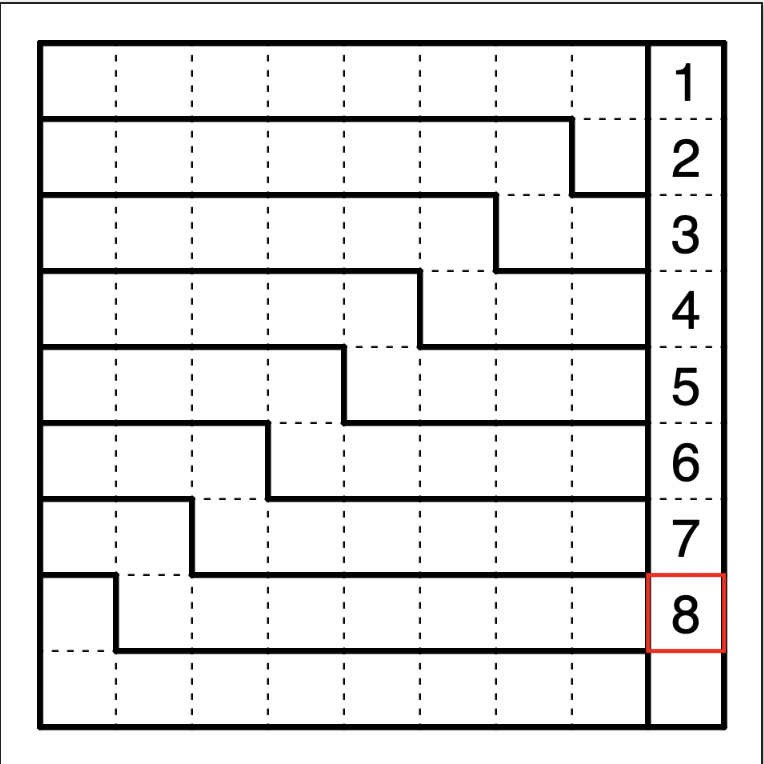
All the 4x4 Sudoku Puzzles
What is a sudoku?
We can split a sudoku puzzle into three parts:
- The solution
- The clues
- The grid
A solution to a 4x4 might look like:
12 34
23 41
34 12
41 23The clues are the subset of the solution that we are allowed to see.
Finally, the grid is typically just a subdivision into 4 boxes covering 4 cells each.
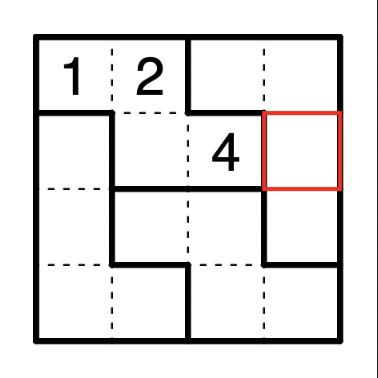
How many 4x4 sudokus are there?
How many solutions are there?
It’s not difficult, but hella annoying, to work out that there are 12. This corresponds to the following OEIS sequence. Ignoring the grid restrictions sudoku is just a “Latin Square” puzzle; fit the numbers 1 to n in an nxn square without having the same number twice in a column/row. There are many possible 4x4 latin squares (576, to be precise).
However, it doesn’t really feel like rotating a latin square by 90° should produce a new latin square - the two squares are still essentially the same. More precisely, we want to account for symmetry. There are 4 types of symmetries that a latin square can have:
- Rotational (4 different types)
- Reflectional (2 different types)
- It might feel like there are more, depending on your axis of reflection - but we can account for this using the rotations, so we really only need one axis of reflection
- Permutational (24 different types)
- We could easily swap every occurance of 1 with 2 and vice versa, but the square is still “the same”. This is permutational symmetry, in which we change which numbers are which but not where they are.
- (24 = 4!)
- Row-permutational (24 different types)
- We can change the order of the rows without changing the latin square
- Column permutations can be done using a rotation first
The first three symmetries all still apply when we add a grid, but the fourth one could destroy our grid by splitting one of our boxes into two disconnected components. Typically we don’t allow this, so I’m treating puzzles that are row-permutationally equivalent to be different.
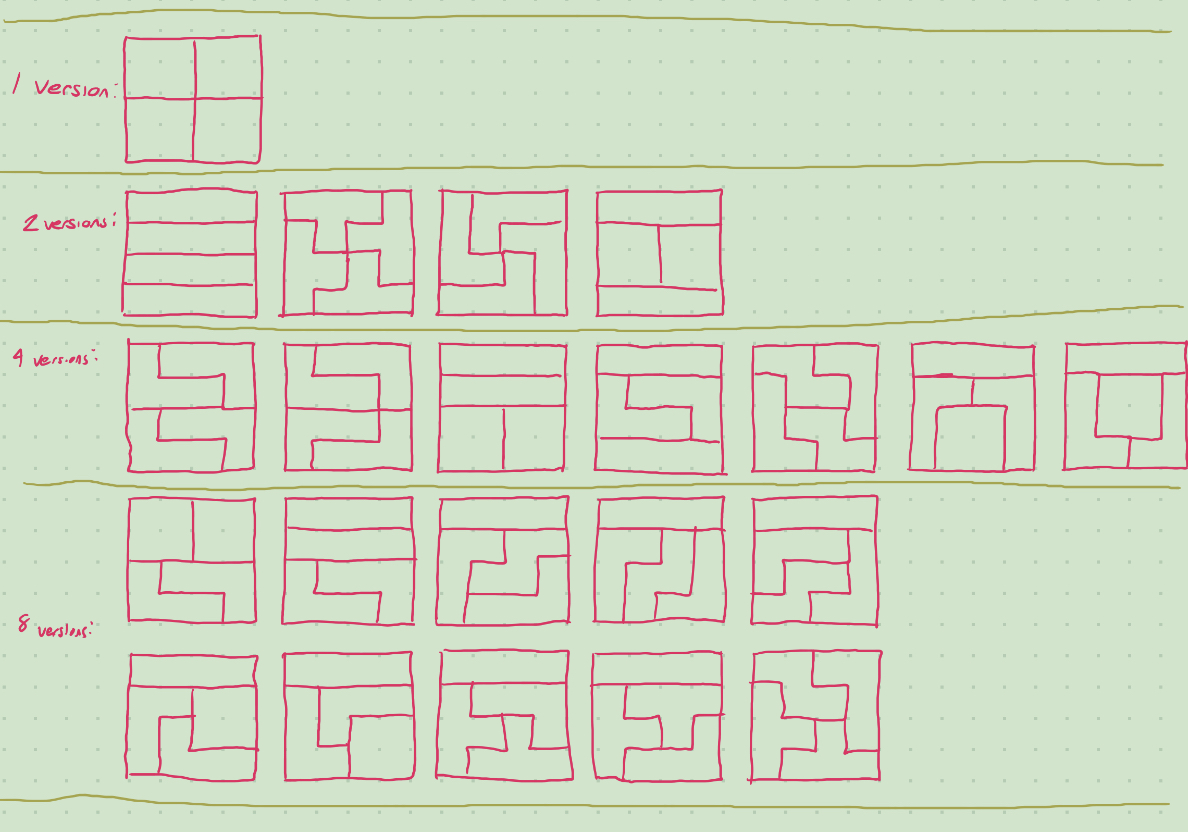
It turns out that there are only 4 different latin squares, accounting for all 4 symmetries - but when we ignore row-permutational symmetries, there are 12 different latin squares. To my knowledge, these are not enumerated anywhere on the internet.
In the above image, I wrote the solutions in a number-agnostic way to emphasize the permutation symmetry.
How many grids are there?
A connected box made of 4 cells is called a “tetromino” (tetra=4, omino as in domino for the 2-cell case). These are exactly the pieces that you use in tetris! The question of how many grids there are can be rephrased as “how many ways can a 4x4 square be decomposed into tetrominos”? For this, I refer the reader to the mayhematics site which has a nice writeup. These are the grids:
Unlike the solutions, we do need to take into account symmetric versions of the grids - this is because we want to combine solutions and grids, so we need to combine them in all orientations. We could have instead done this with the solutions, and only considered the 22 fundamental grids. Instead we have 117 grids, although I won’t write them all out.
How many solution-grid pairs are there?
This gives us 12 * 117 = 1404 possible pairs… except that not every grid is compatible with every solution. The first solution I gave is incompatible with the first grid, for example.
TO BE CONTINUED
What is the minimal amount of clues for each solution/grid pair?
This problem has a few related problems:
- For a given solution, what is the minimal amount of clues needed among all possible grids
- Likewise, what is the minimal amount of clues needed for some grid with that solution
- For a given grid, what is the minimal amount of clues needed among all possible solutions
- Likewise, what is the minimal amount of clues needed for some solution on that grid
For the standard grid, it is known that there exists a solution where 4 clues is minimal. It is not too hard to construct a grid such that there exists a solution where 3 clues is minimal:

In fact no puzzle could ever require less than three clues, due to permutation symmetry (if two of the numbers are unspecified, for example 1 and 2, then there is nothing in the clues that fixes which one is which - you could swap them and still have a valid solution to the clues on the grid).
Generalizing to nxn
In general, for an nxn sudoku with n symbols to place, there is never a puzzle (with a unique solution) that gives only n-2 clues. Less trivially, but still not too hard to see, is that there is always a puzzle that requires only n-1 clues.